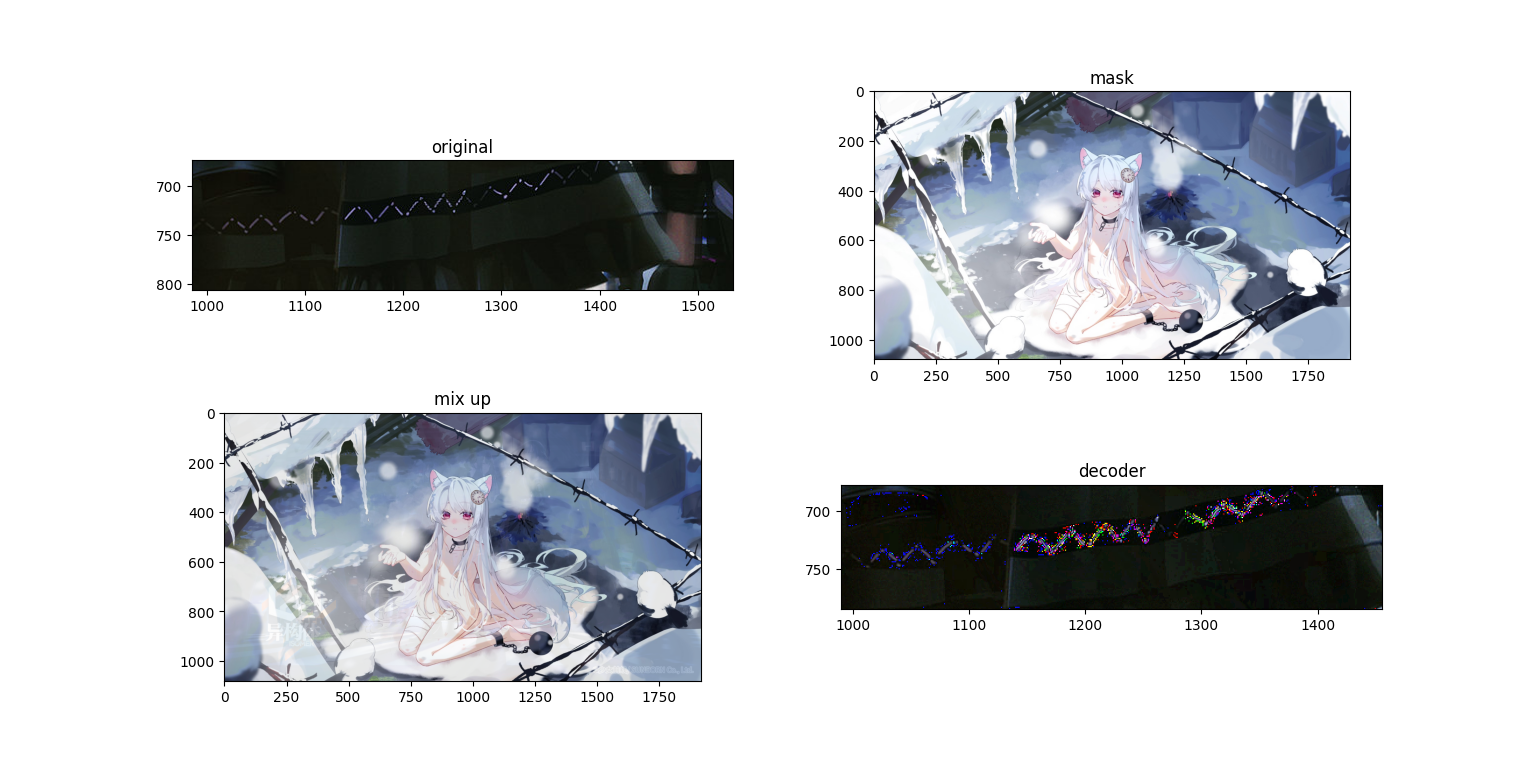
 粗看没有什么问题,但是我们把图像放大
粗看没有什么问题,但是我们把图像放大
 会发现在混合图(第三张,mix up)上面隐约有能看到原图,而求解出来的图上面又有一些噪点,接下来再看一组图
会发现在混合图(第三张,mix up)上面隐约有能看到原图,而求解出来的图上面又有一些噪点,接下来再看一组图(哈哈 这个排版 稀烂咯)
我将实验几种算法方法,试图实现简单的图像隐写,或者说“幻影坦克”,我需要寻找可靠性高(抗干扰抗压缩)、计算量小的算法来规避B站的直播系统,加密时只要肉眼看不出问题,解密时只要肉眼能看得出就彩六即可。目前我考虑两种算法,一是原本用于数据增强的mix up算法,他是简单的线性叠加,但是也由于其线性使其很容易逆转;二是后门攻击《Hidden Trigger Backdoor Attacks》中提到的方法,其原本用于隐藏带有触发器的图片;三是基于缩放的方法(准确的说近邻法),也就是将底图按像素替换mask的一部分,解码就只需要删除特定行列即可;四是末位置0法(准确的说应该是LSB),他实质上是对图的二进制形式进行修改,和mix up类似,但是他解码时不需要知道mask,缺点是不抗压缩;五是基于小波变换,将图片藏到频域;六是基于稀疏表示。除此以外,我可能考虑将图像转为灰度图以减少计算的难度,以及将声音编码进图像中,测试一张图像能叠加多少内容(提高容量可以让我们把一张高清图拆解之后塞进小图里面),检查其在频域的变化,抗干扰测试和抗压缩测试,图像校验和修复。
孩子不懂事,瞎搞来玩的。不是正经研究,不要问为什么不计算峰值信噪比之类的,本来就是人眼看不出来就行了。有问题不要问作者,作者也不懂。不要试图用这些方法做任何违法违规的事情,对于正儿八经的隐写或者盲水印检测,这些都太落后了。
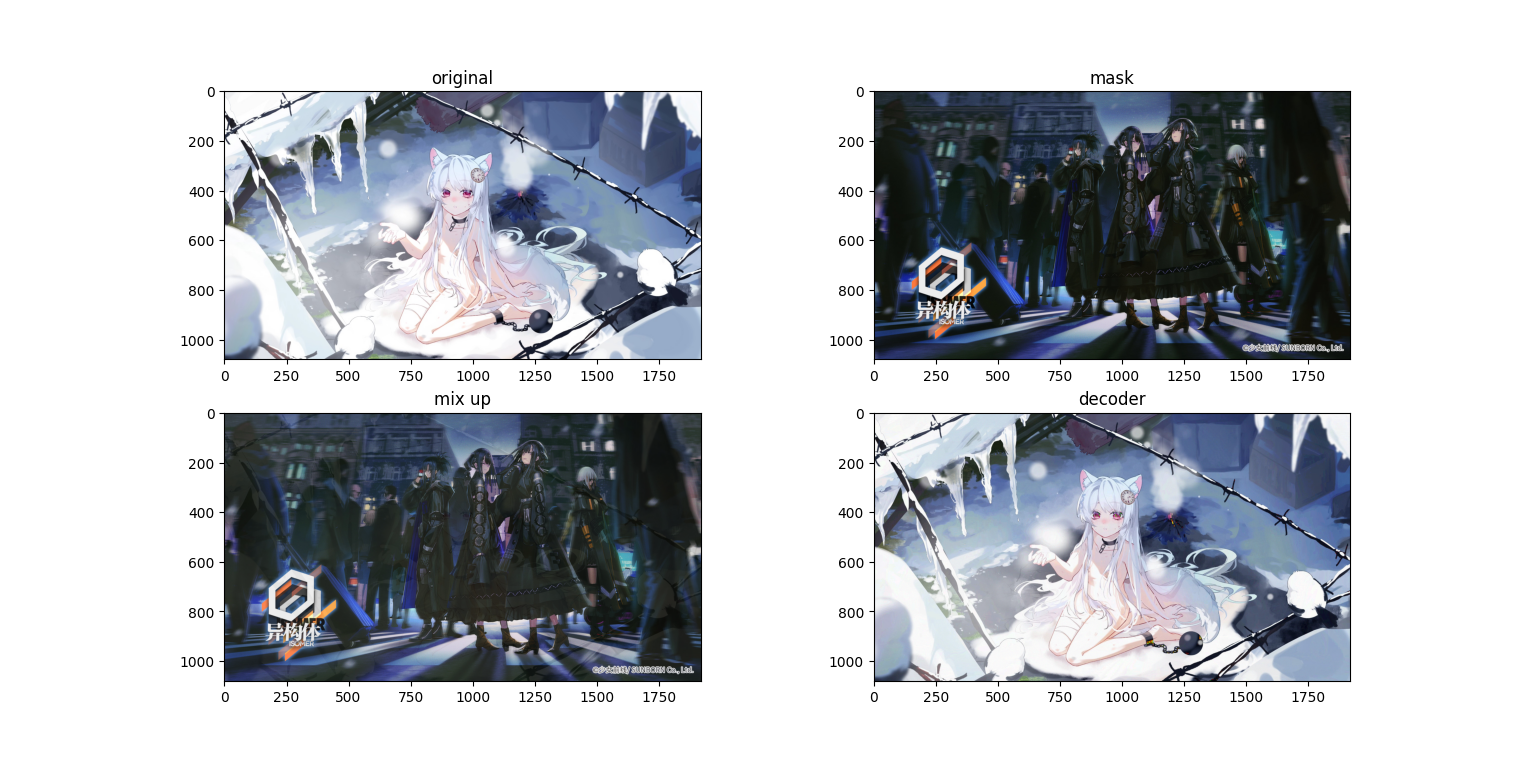
mix up是一种简单的线性叠加,其表达式可以为$imout=im\times lam+mask\times (1-lam)$,在原本的应用中lam应该是一个随机数矩阵,但是在我们的应用中我们将使用一个固定的数,我们取0.1,因此对应的解码就是$im=(imout-mask\times (1-lam))\div lam$,我们使用代码:
lam=0.1#encoder
im_mixup=(im1*lam+im2*(1-lam)).astype(uint8)
plt.subplot(2,2,3),plt.title("mix up"),plt.imshow(im_mixup)
#decode
plt.subplot(2,2,4),plt.title("encoder"),plt.imshow(((im_mixup-im2*(1-lam))/lam).astype(uint8))
plt.show()
(是不是很简单)
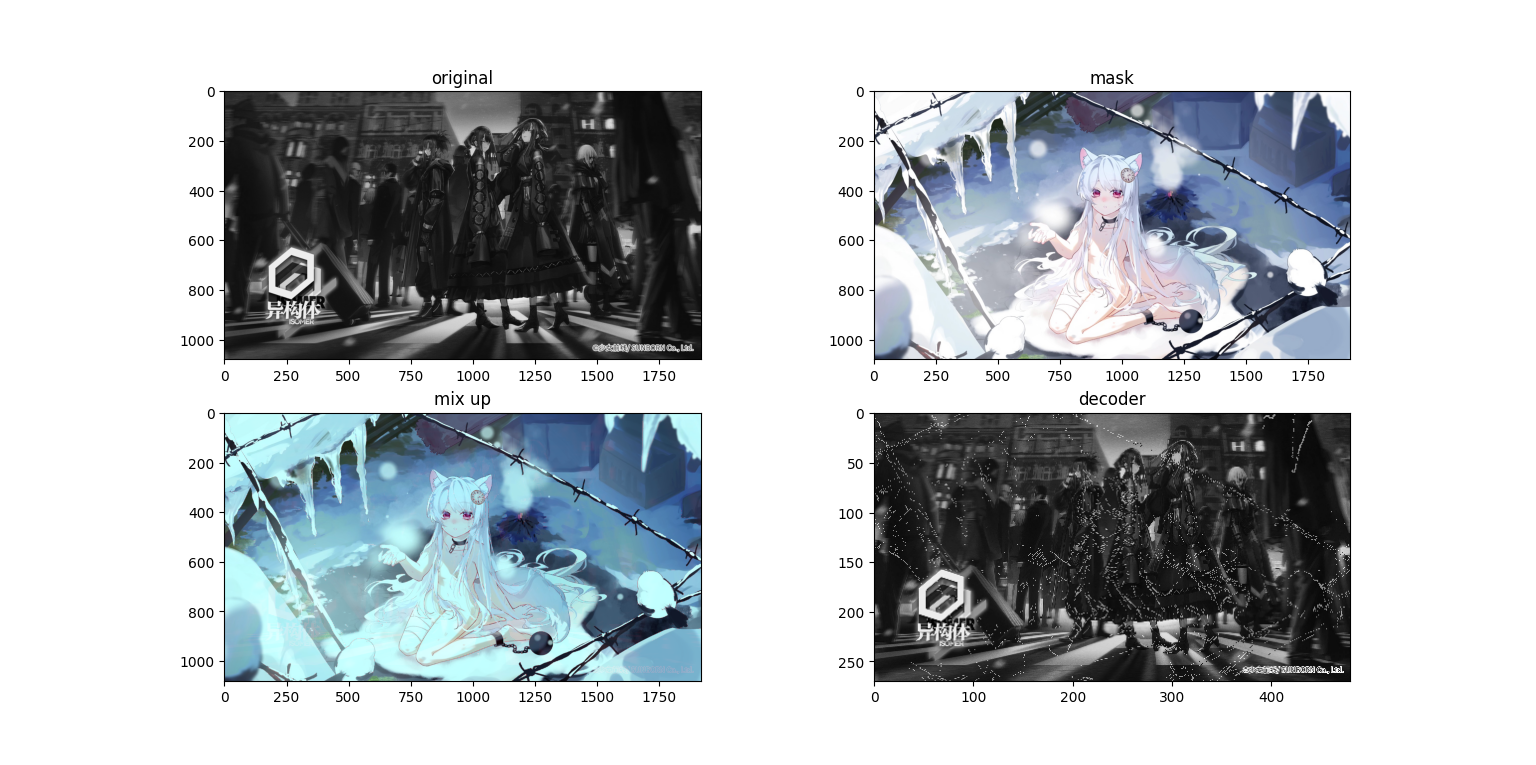
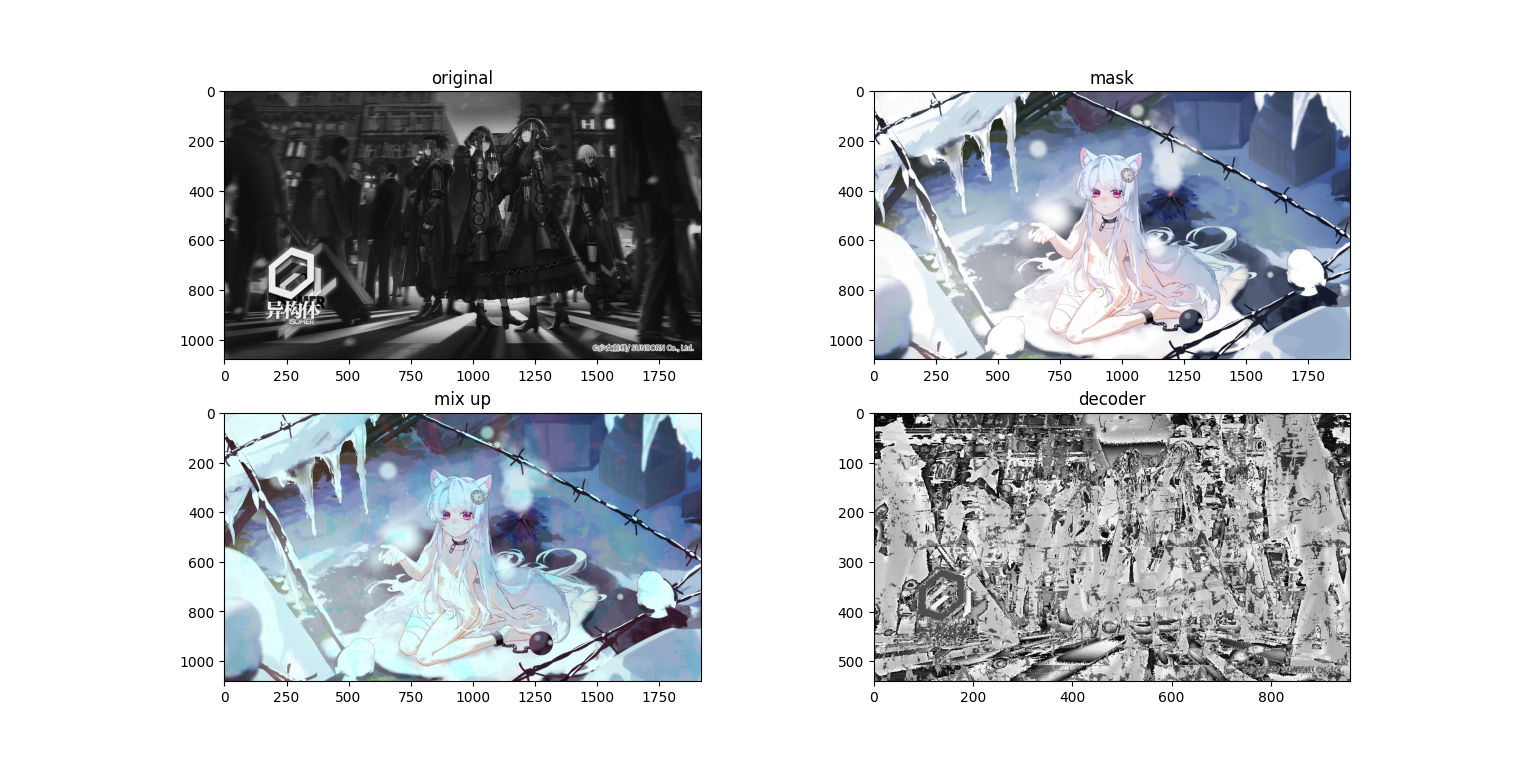
我们使用1920×1080的图片进行实验,接下来看看运行结果
 粗看没有什么问题,但是我们把图像放大
粗看没有什么问题,但是我们把图像放大
 会发现在混合图(第三张,mix up)上面隐约有能看到原图,而求解出来的图上面又有一些噪点,接下来再看一组图
会发现在混合图(第三张,mix up)上面隐约有能看到原图,而求解出来的图上面又有一些噪点,接下来再看一组图
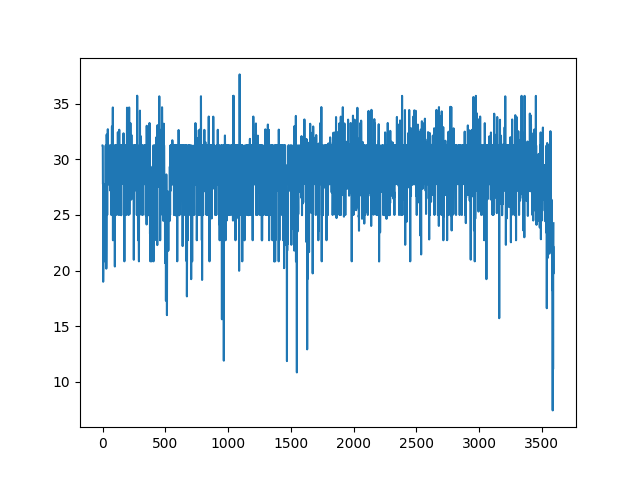
顺便一提,雪狐真可爱,嘿嘿
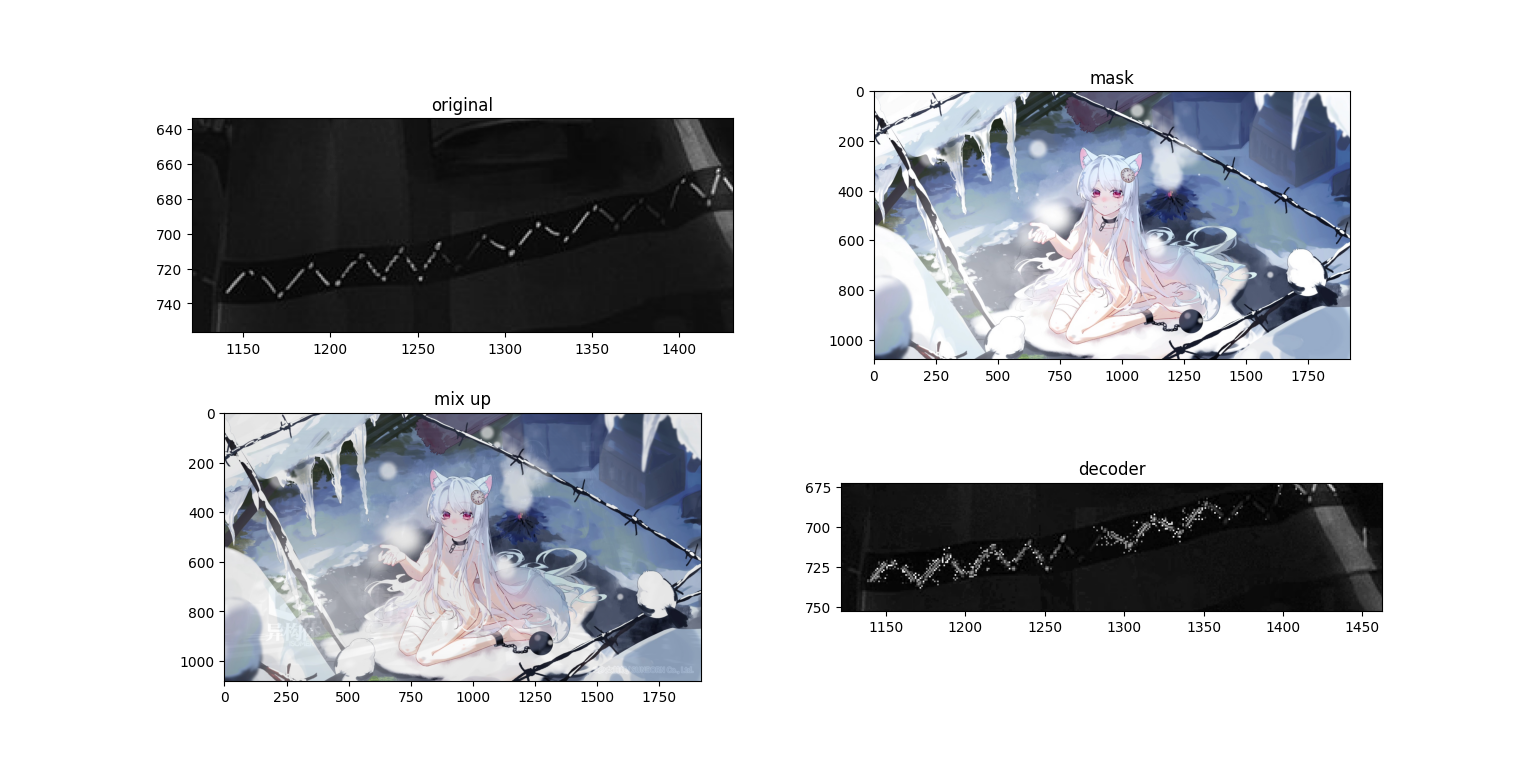
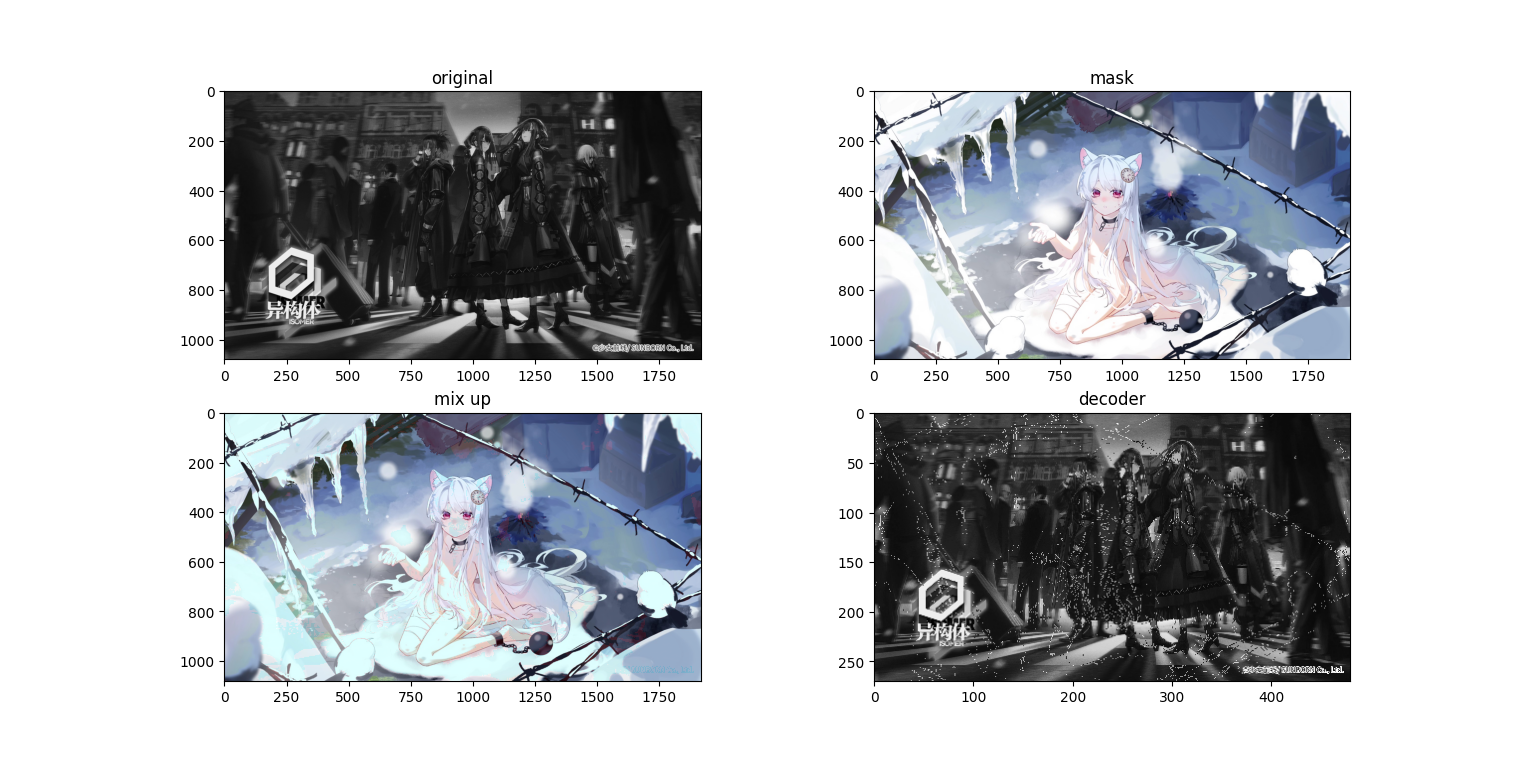
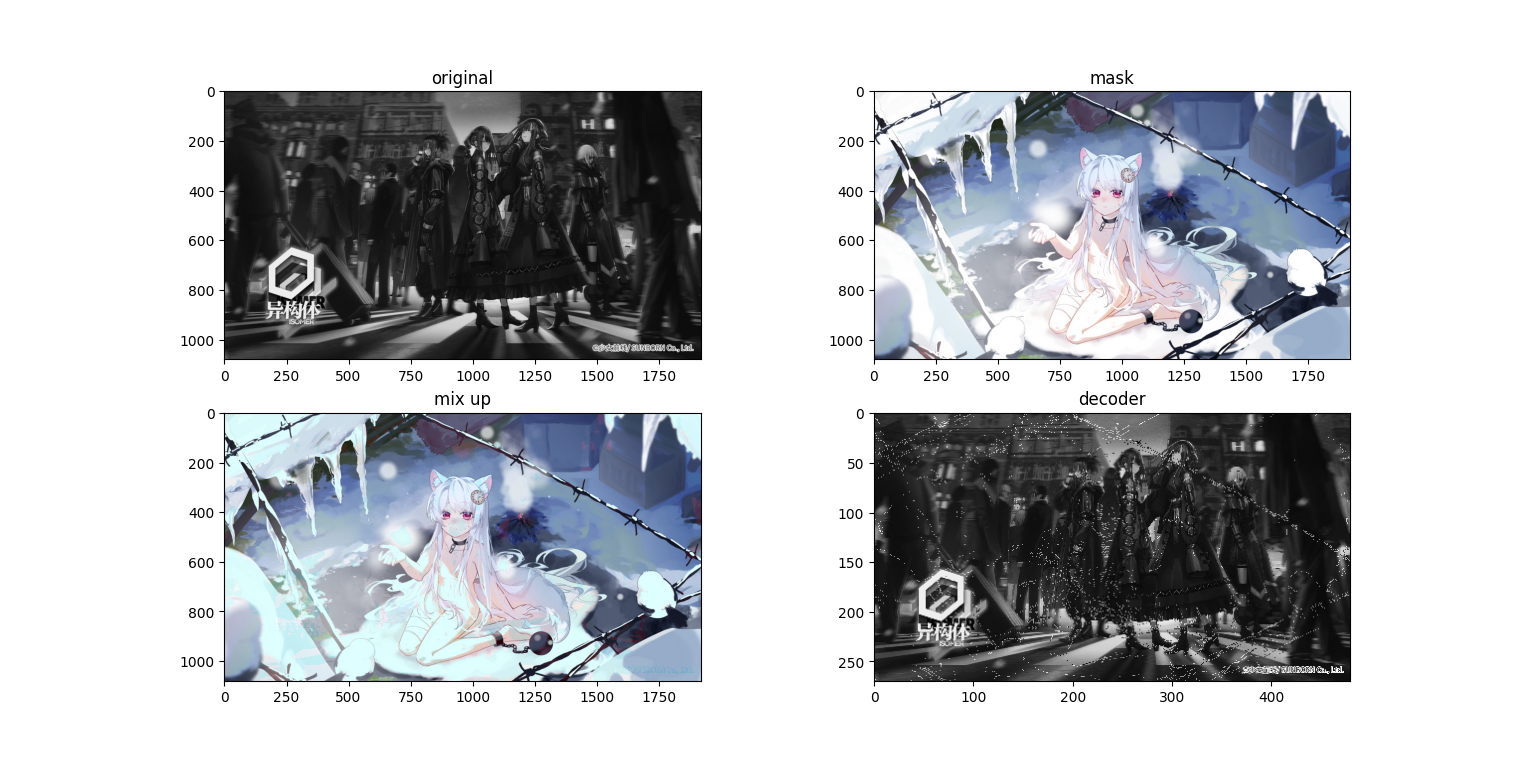
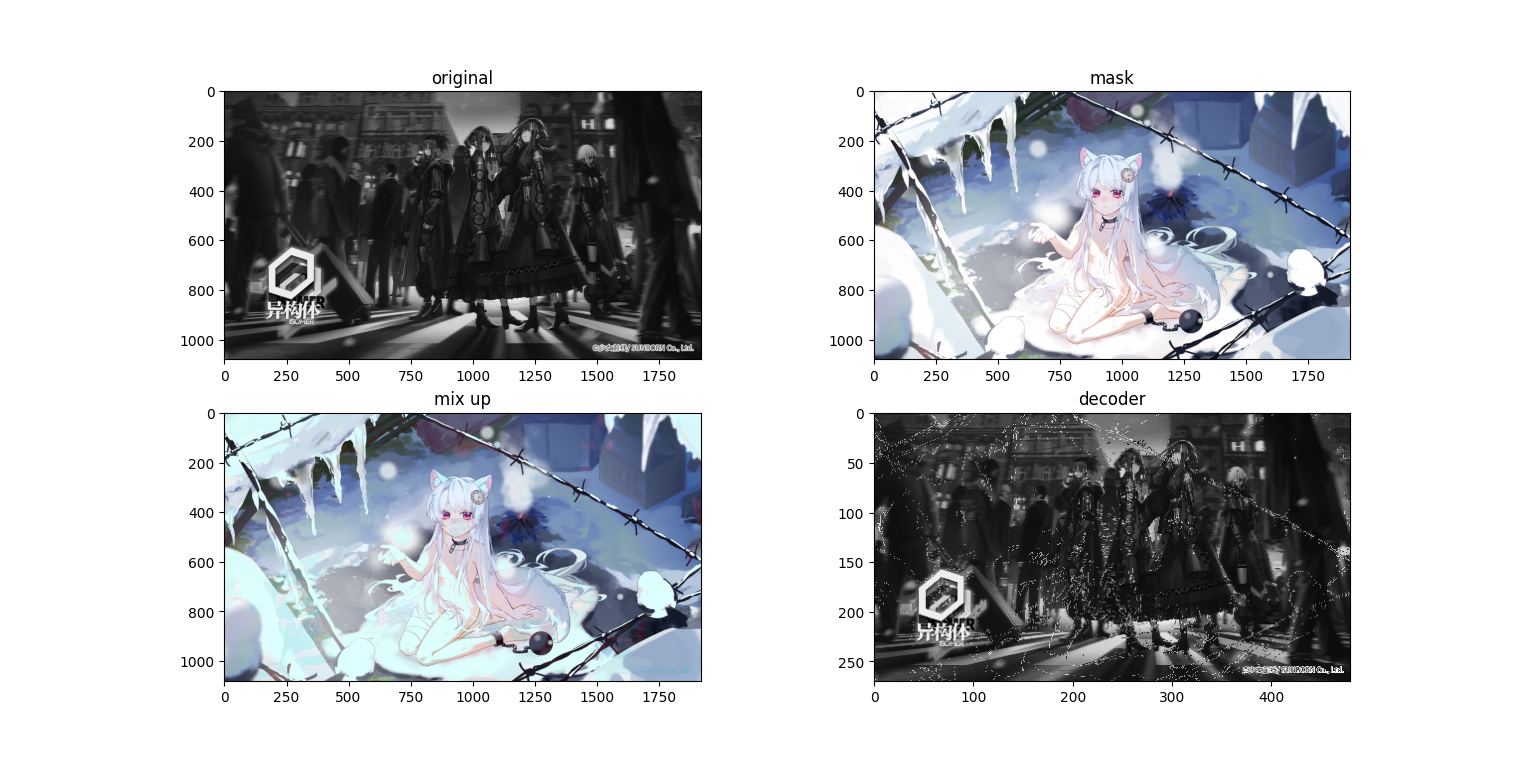
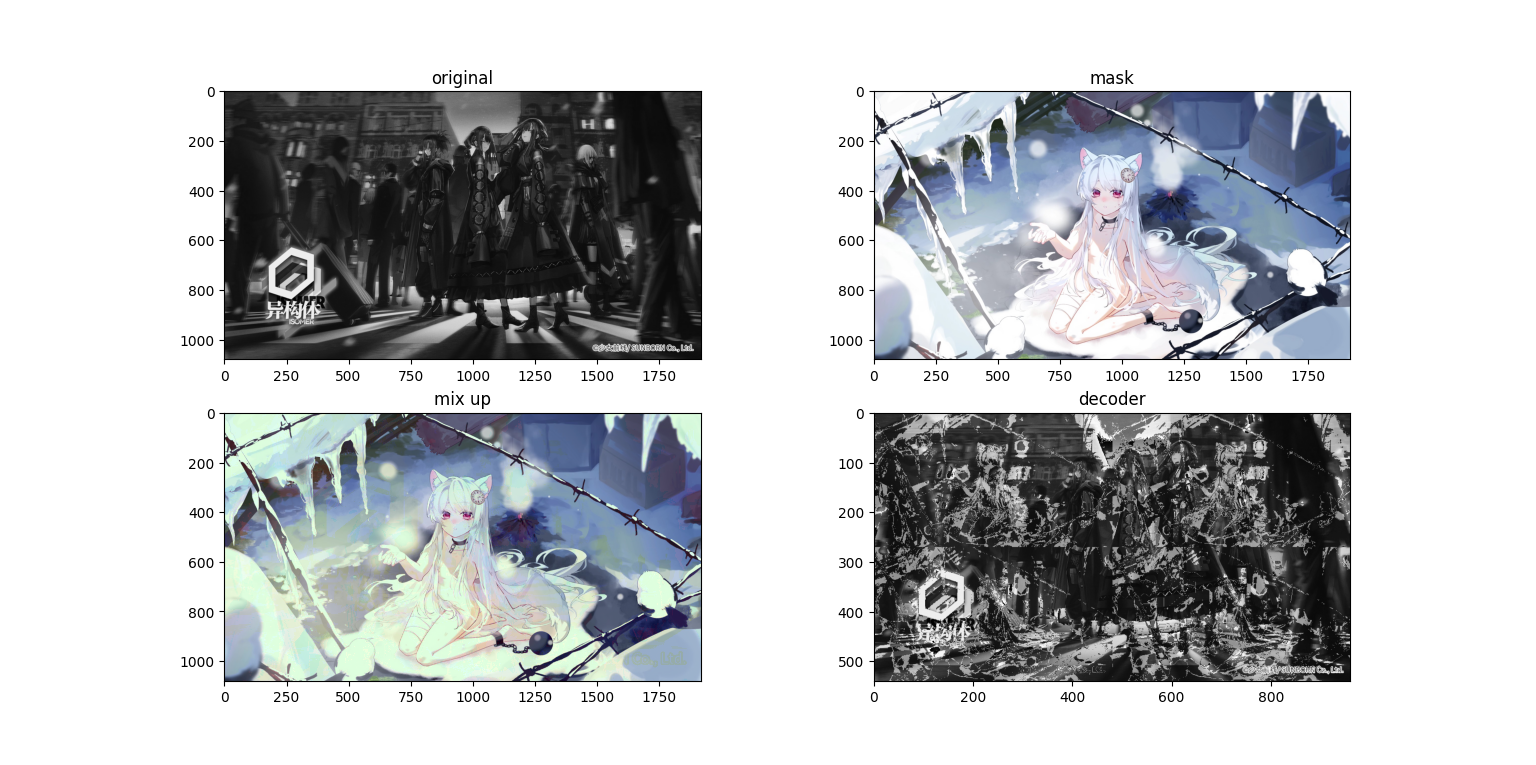
 可以看到在浅色mask的情况下的深色内容十分明显,如果变成动态的则更加显眼,同时在色块边缘,特别是颜色变化较大的地方(应该是梯度较大?等下做个RGB的梯度分析吧)杂色更多,可能是还原时小数计算导致的。那么接下来我们试着把原图处理成灰度图。
可以看到在浅色mask的情况下的深色内容十分明显,如果变成动态的则更加显眼,同时在色块边缘,特别是颜色变化较大的地方(应该是梯度较大?等下做个RGB的梯度分析吧)杂色更多,可能是还原时小数计算导致的。那么接下来我们试着把原图处理成灰度图。
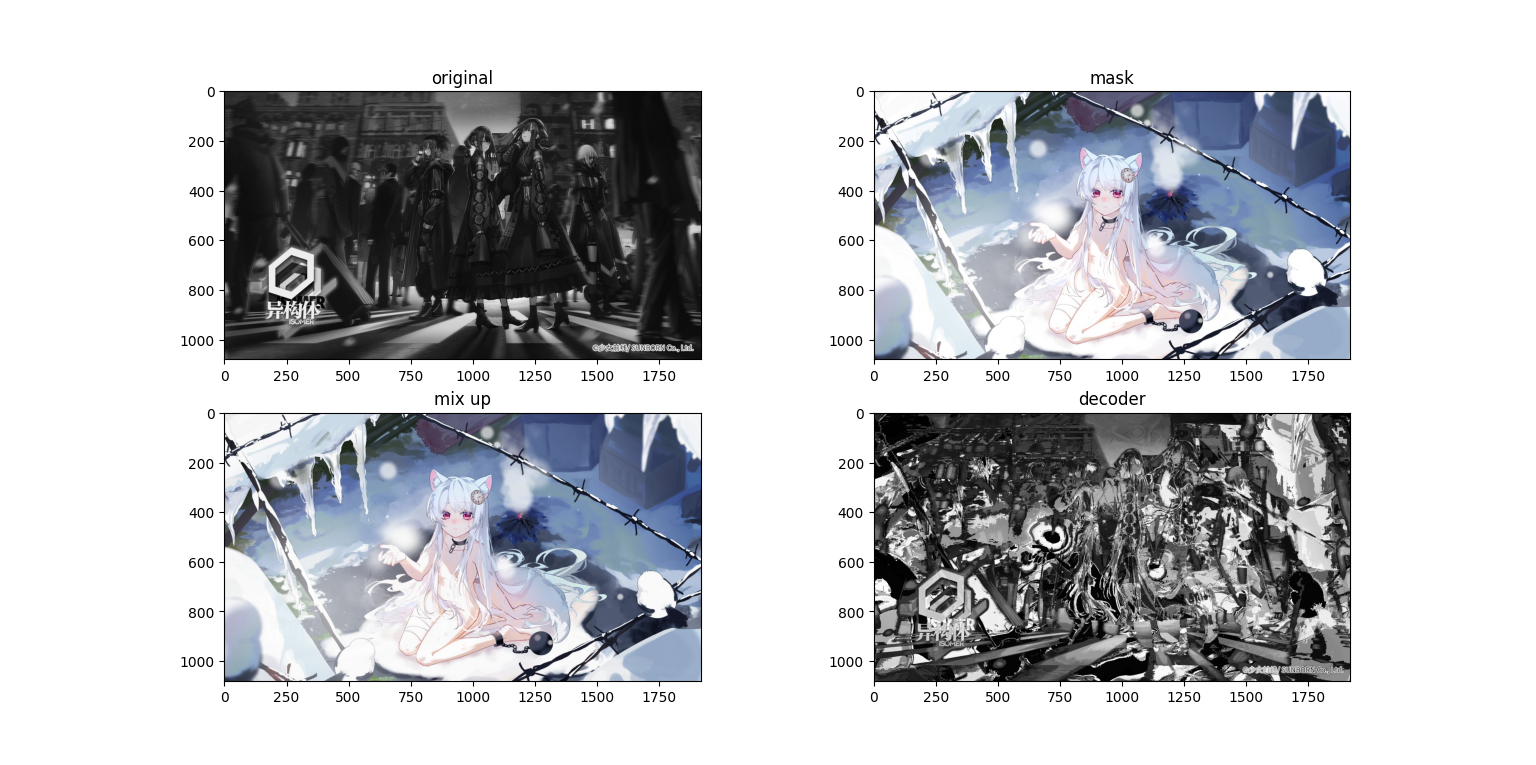
 看起来好了点,但是有些地方还是可以透过mask看到内容。如果我们把内容图的占比,也就是
看起来好了点,但是有些地方还是可以透过mask看到内容。如果我们把内容图的占比,也就是lam降低呢?
 这里使用了
这里使用了lam=0.02,可以看到,“异构体”的图标确实不见了,但是求解出来的图像基本上失去了内容,目前测试来看0.05以上比较合适(上面一行是叠加图,下面一行是还原图),不过说起来,之后可以根据灰度图的差值优化出一个更优的lam。同时我们还记录了每一次叠图+解析的耗时,显示在图片下方,平均下来这个过程耗时约0.2s(使用i5-7200U@2.50GHz运行)
 再来看看以
再来看看以lam=0.1时,进行mix up后他们在频域上的变化(应该是看不出来关系的)
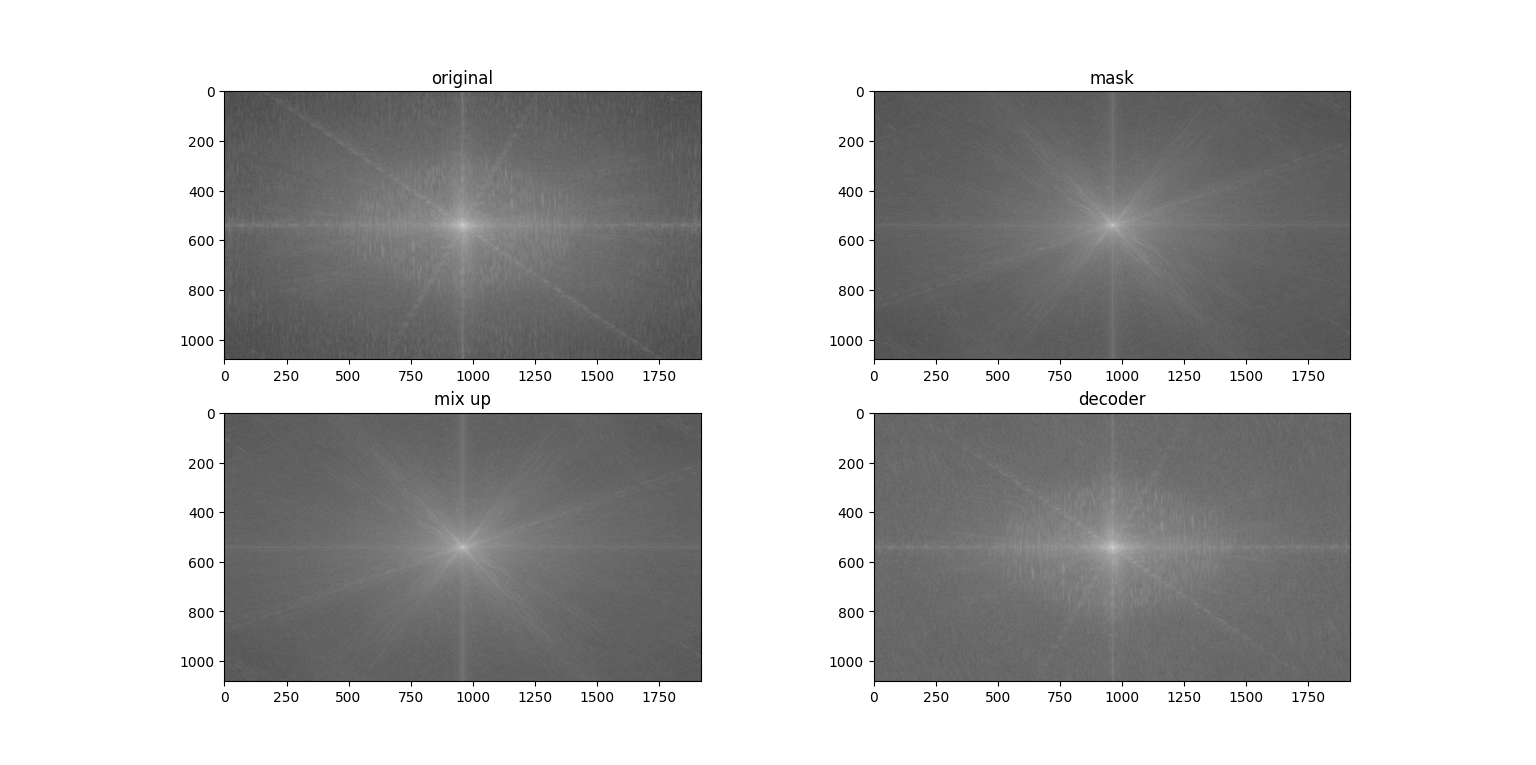 关于抗干扰,从理论上来说,线性叠加是不抗压缩的,但是因为这个算法对于压缩不敏感,特别是灰度之后(不像频域),所以观感上差别不大。如下是通过对mix_up压缩一定比例之后用立方插值(
关于抗干扰,从理论上来说,线性叠加是不抗压缩的,但是因为这个算法对于压缩不敏感,特别是灰度之后(不像频域),所以观感上差别不大。如下是通过对mix_up压缩一定比例之后用立方插值(cv2.INTER_CUBIC)重新恢复大小再用正确的mask进行解码的结果
 我靠,打脸了,这里模拟压缩之后等效于mask的图形范围变大,覆盖了不少原图。那应用的时候得想办法减少压缩比例才行。或者我们找到这个确切的压缩比例,在还原时也对mask进行压缩或者模糊,通过下图可以看到对于压缩比例不大的情况还是挺有效的:
我靠,打脸了,这里模拟压缩之后等效于mask的图形范围变大,覆盖了不少原图。那应用的时候得想办法减少压缩比例才行。或者我们找到这个确切的压缩比例,在还原时也对mask进行压缩或者模糊,通过下图可以看到对于压缩比例不大的情况还是挺有效的:
 处理完了图片,我们来看看处理视频的能力,这里主要是看进行叠视频和解视频的耗时,这里以两个分辨率相同长度2分钟的B站视频为例。下图是进行叠图时的实时帧率(用1除以计算时长得到,其中计算时长包括了加密和解密两个过程),两个原视频都是30帧的,实时帧率基本上在25~30帧附件波动(使用i5-7200U@2.50GHz运行),应用时可能要考虑抽帧或者优化算法。
处理完了图片,我们来看看处理视频的能力,这里主要是看进行叠视频和解视频的耗时,这里以两个分辨率相同长度2分钟的B站视频为例。下图是进行叠图时的实时帧率(用1除以计算时长得到,其中计算时长包括了加密和解密两个过程),两个原视频都是30帧的,实时帧率基本上在25~30帧附件波动(使用i5-7200U@2.50GHz运行),应用时可能要考虑抽帧或者优化算法。
结论:对图像进行灰度化后,使用颜色比较混杂的(比如色系相反)图作为mask,以接近0.1的比例进行叠图是可行的,并且编码解码速度较快。缺点是用户必须知道mask和lam,而且最好知道压缩情况。
近邻法就是简单的替换掉固定区域的像素,因此mask和底图面积大小最好是四倍之类的整数倍关系。然后考虑直接用列表切片不用for循环,这样子计算时间能降不少,关键代码如下:
if im1.shape[0]*sizes!=im2.shape[0] or im1.shape[1]*sizes!=im2.shape[1]:
im1=cv2.resize(im1,(im2.shape[1]//sizes,im2.shape[0]//sizes))
#encoder
mixup=im2.copy()
mixup[:mixup.shape[0]:sizes,:mixup.shape[1]:sizes]=im1
#decode
decode=mixup[:mixup.shape[0]:sizes,:mixup.shape[1]:sizes]
return mixup,decode
运行结果如下
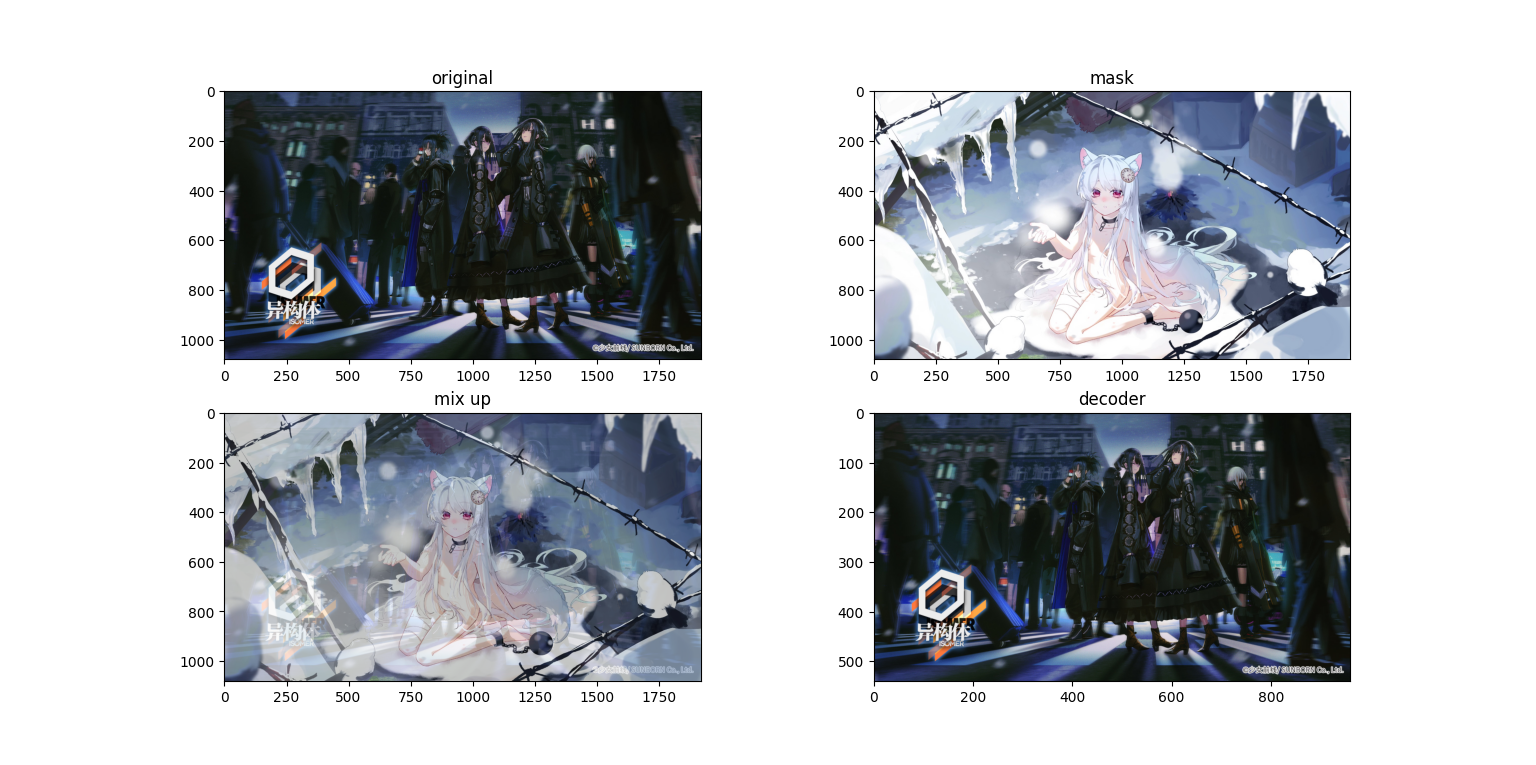 做一个简单的傅里叶变换,可以看到解码出来的图被“放大”了,以及混合时的频域图有多个中心
做一个简单的傅里叶变换,可以看到解码出来的图被“放大”了,以及混合时的频域图有多个中心
问题也很明显,如果sizes(控制几乘几个像素为一个单元)太小,隐写太明显,sizes太大,原图压缩太多变糊。我们做了一组测试,第一行是sizes,第二行是混合后的图,第三行是解析出来的图,第四行是运行时间(包括编码解码),可以看到比mix_up快了不少。目前来看sizes选3和4会比较合适

至于抗压缩嘛,这种直接插进像素的方法本身就相当于加噪声,基本上一压缩就没救了。下面是sizes=4时,压缩后复原的结果,基本上就是无法复原

算了,直接看视频的处理情况吧,下图是每帧计算耗时,是挺快的,估计是少了灰度化这类的计算吧。一开始我也想计算帧率的直到他告诉我不能除以零,虽然不知道为什么,但是确实time.time()函数读到的时间差就是0,基本上都在0.005秒内(使用i5-7200U@2.50GHz运行)。
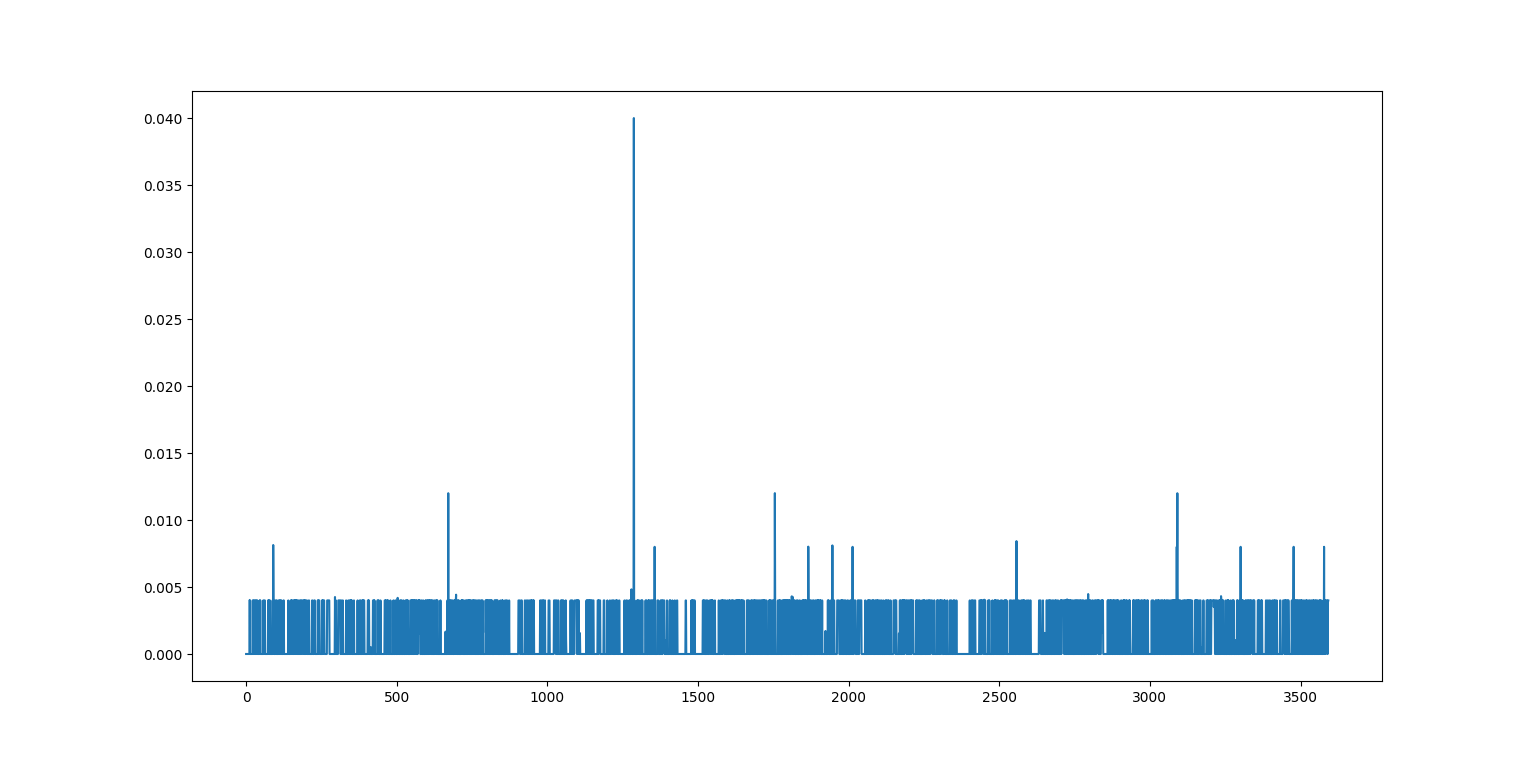
结论就是近邻法运算速度极快,但是信息容量小而且不抗压缩和模糊,可以用这些多出来的时间对原图做点什么。
简单来说就是,一个像素的RGB中的一个分量不是一个八位的二进制嘛,如果删掉最后面的三位,也就是相当于约成8的倍数(至多-7),从视觉上可能效果差不多,删掉的这三位用底图的前三位来替换,G和B通道以此类推,但是B只改两位(不过具体是332还是别的方法,别人有测,先逝世罢)。涉及位运算嘛,所以直接生成模板图来进行cv2的图位运算(而且反正是相同值的模板图,可以拉伸,但是还是先研究$1920\times 1080$的。模板图推算过程如下:
$([R,G,B]\And[248,248,252]) | \big((T\And[224,28,3])\div[32,4,1]\big)$
$([R,G,B]\And[0b11111000,0b11111000,0b11111100]) | \big((T\And[0b11100000,0b00011100,0b00000011])\div[0b00100000,0b00000100,0b00000001]\big)$
$\big((S\And[7,7,3])[32,4,1]\big) \quad \text{#解码过程}$
$\big((S\And[0b00000111,0b00000111,0b00000011])[0b00100000,0b00000100,0b00000001]\big) \quad \text{#解码过程}$
其中T是底图的灰度图,是一个深度为3的包含8位二进制的矩阵(就是对灰度图进行拓展到三个通道),如下是关键代码:
def bits(im1,im2,W:list):
mixup=(im1&W[0])|((im2&W[1])//W[2])
decode=(mixup&W[3])*W[2]
decode=np.sum(decode,axis=2)#因为输入是灰度图,这里解算也重新合成为灰度图
return mixup,decode
def generate():
w1=np.repeat(np.repeat([[248,248,252]],1920,axis=0),1080,axis=0)
w2=np.repeat(np.repeat([[224,28,3]],1920,axis=0),1080,axis=0)
w3=np.repeat(np.repeat([[32,4,1]],1920,axis=0),1080,axis=0)
rw1=np.repeat(np.repeat([[7,7,3]],1920,axis=0),1080,axis=0)
return [w1,w2,w3,rw1]
三通道的灰度图我们是通过cv2灰度化然后用np去叠出来的
im1=cv2.cvtColor(im1,cv2.COLOR_BGR2GRAY)
im1=np.stack((im1,im1,im1),axis=-1)
运行结果和傅里叶变换如下,可以看到和之前的方法相比,无论是空间域还是频域,mask都没有明显的变化,解析的效果也非常好:
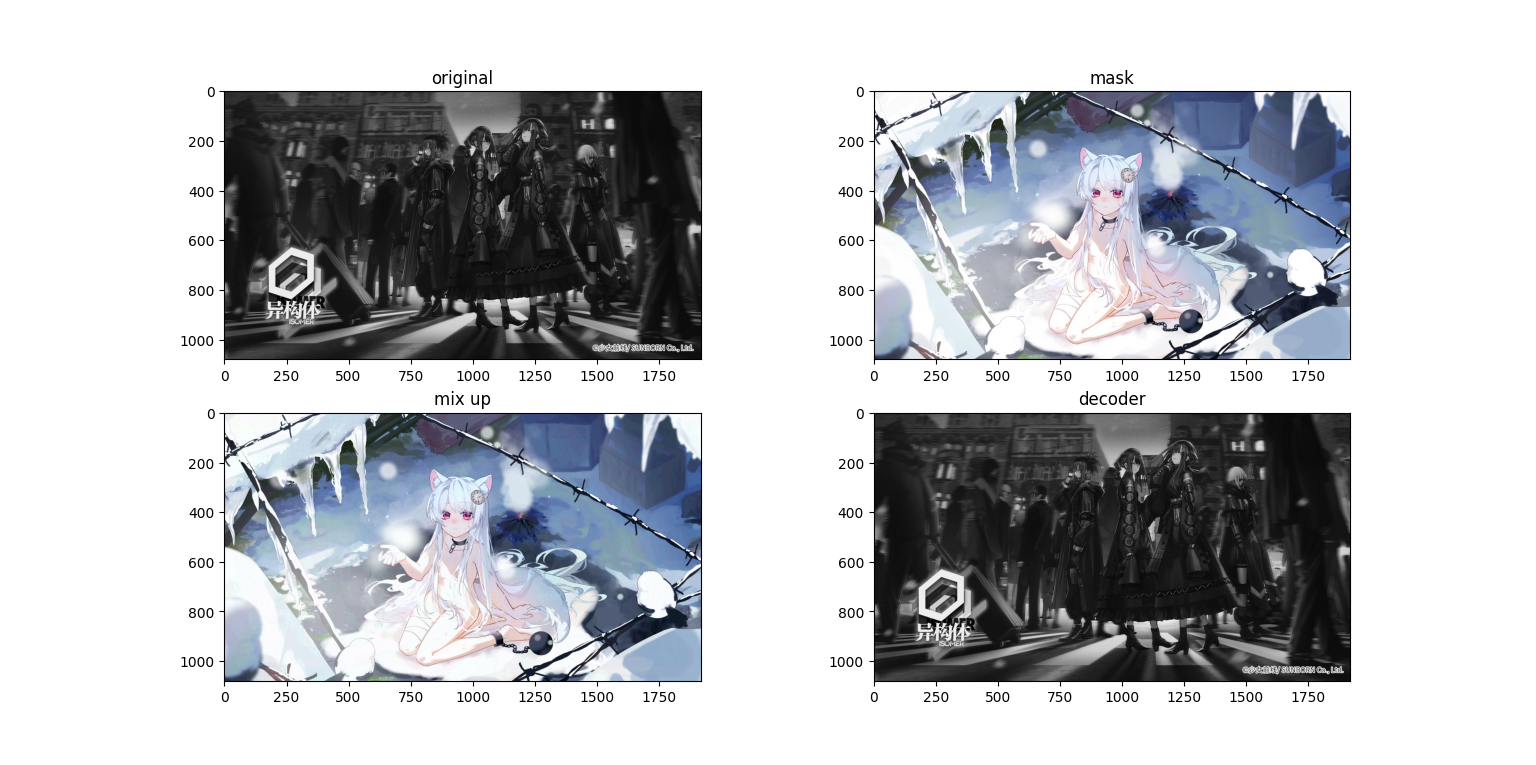
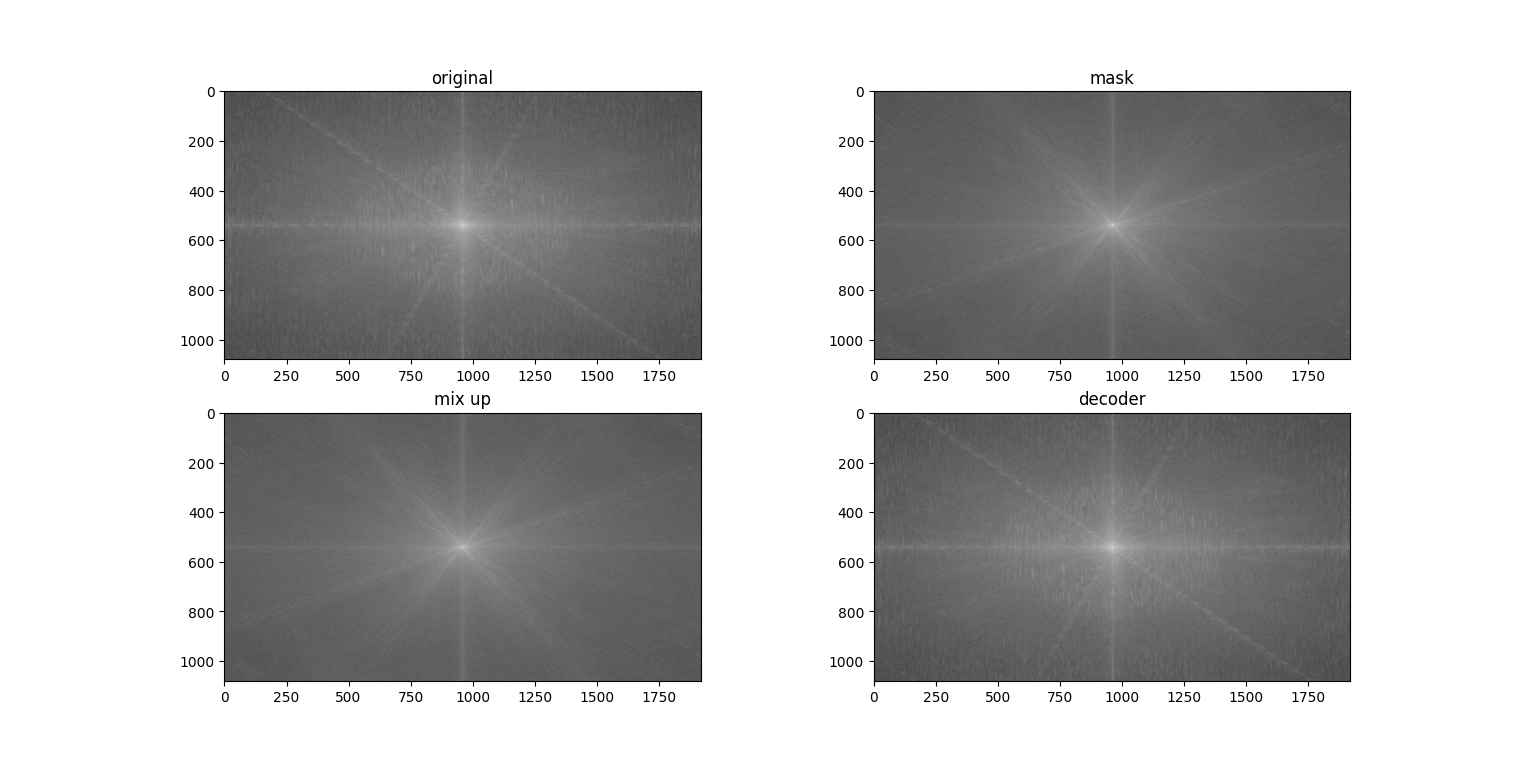 LSB可调的参数特别少,无非是优化计算流程,调整运算模板的值,所以我们直接来看看抗压缩吧,按理说LSB应该不怎么抗压缩,毕竟后几位很容易被模糊掉。
LSB可调的参数特别少,无非是优化计算流程,调整运算模板的值,所以我们直接来看看抗压缩吧,按理说LSB应该不怎么抗压缩,毕竟后几位很容易被模糊掉。
 算了,还是看看视频隐写的情况吧,基本上能保证30帧(使用i5-7200U@2.50GHz运行)。
算了,还是看看视频隐写的情况吧,基本上能保证30帧(使用i5-7200U@2.50GHz运行)。
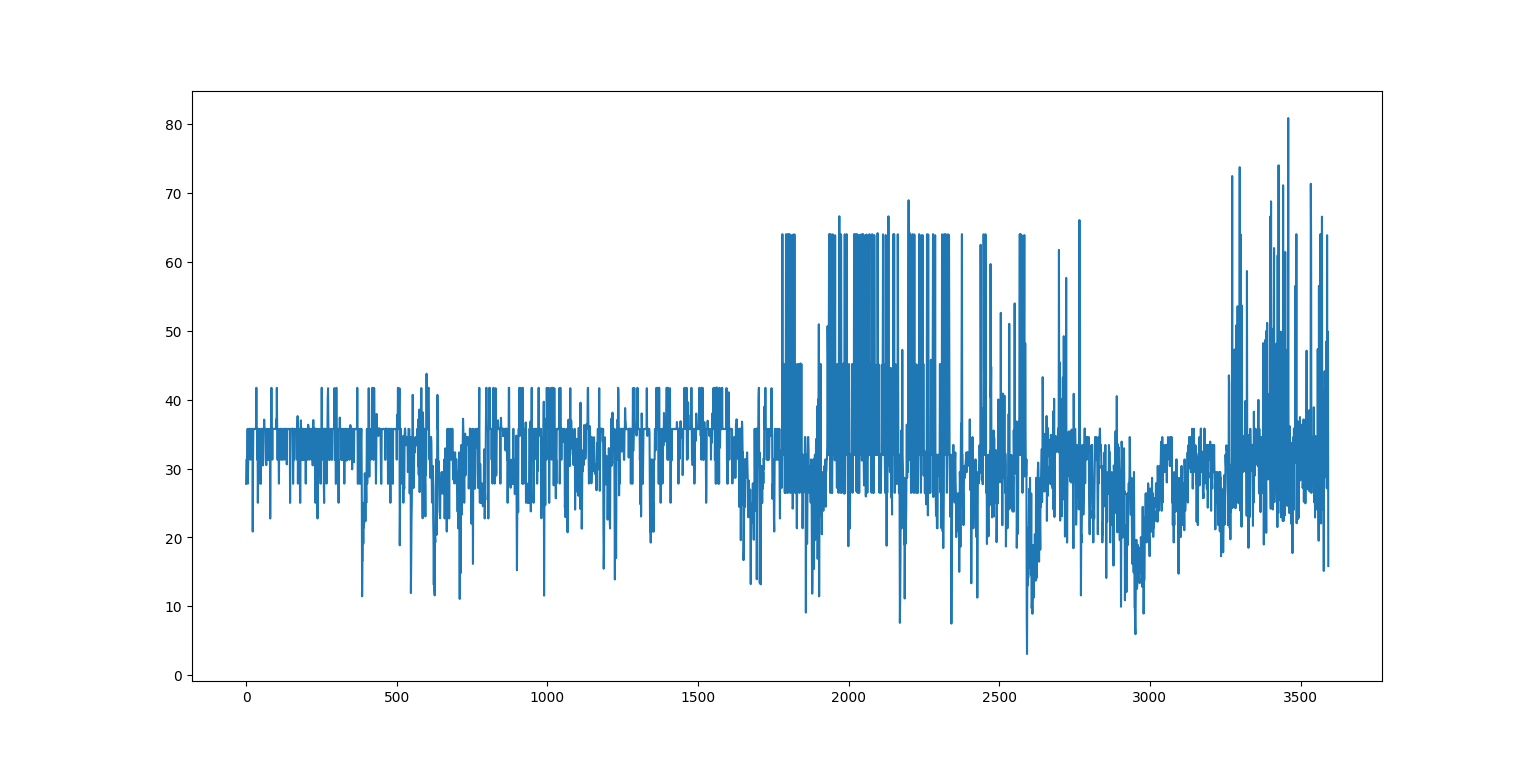 结论就是LSB作为经典隐写算法,隐蔽效果好(从肉眼的角度来说)但是也不抗模糊,而且目前运算速度也比较感人,应该可以再优化。
结论就是LSB作为经典隐写算法,隐蔽效果好(从肉眼的角度来说)但是也不抗模糊,而且目前运算速度也比较感人,应该可以再优化。
就是基于离散小波变换(DWT)的图片隐写,小波变换可以理解为以小波基为基的傅里叶变换,对比于傅里叶变换,据说可以更好的隐藏信息,直接把信息藏在特定的频率范围内。我将先尝试把数据转换到频域之后用近邻法来替换,关键代码如下:
imL=list(cv2.split(im2))
y,x=im1.shape
cA,(cH,cV,cD)=dwt2(imL[channel],"haar")
cA=replacePixels(im1[:y//2,:x//2],cA,sizes=sizes)[0]#左下角
cH=replacePixels(im1[:y//2,x//2:],cH,sizes=sizes)[0]#右下角
cV=replacePixels(im1[y//2:,:x//2],cV,sizes=sizes)[0]#左上角
cD=replacePixels(im1[y//2:,x//2:],cD,sizes=sizes)[0]#右上角
mixchannel=idwt2((cA,(cH,cV,cD)),"haar")
imL[channel]=mixchannel
mixup=np.stack(imL,axis=-1).astype(np.uint8)
cA,(cH,cV,cD)=dwt2(cv2.split(mixup)[channel],"haar")
decode=np.vstack((np.hstack((cA[::sizes,::sizes],cH[::sizes,::sizes])),np.hstack((cV[::sizes,::sizes],cD[::sizes,::sizes])))).astype(np.uint8)
这里使用Haar小波基,对图片的某一个通道进行DWT后会得到4张子图,分别是低频分量和三个方向高频分量,我首先选用了R通道(R的补色是蓝色,人眼对于蓝色不怎么敏感,而且mask是蓝白色作为主色的,看下结果:
 可以看到,在低频域颜色变化比较明显,而其他域还好,但是这只是在蓝白主色的图片下的R通道,如果用其他图片的其他通道,色差会非常明显,而且复原图也有一些规律的噪点,且压缩严重。于是我考虑到将图分为四份,将底图切成四份叠加进去,看下结果
可以看到,在低频域颜色变化比较明显,而其他域还好,但是这只是在蓝白主色的图片下的R通道,如果用其他图片的其他通道,色差会非常明显,而且复原图也有一些规律的噪点,且压缩严重。于是我考虑到将图分为四份,将底图切成四份叠加进去,看下结果
 效果更差了,基本上无法复原,应该是因为叠加之后四份图相互干扰了,接下来我考虑用R和B通道的cH和cV进行隐藏:
效果更差了,基本上无法复原,应该是因为叠加之后四份图相互干扰了,接下来我考虑用R和B通道的cH和cV进行隐藏:
 可以看到,色差很明显,修复也很拉胯,我们来看看DWT究竟是什么样的变换,这里对图片的B通道进行了DWT,其中b是逆DWT之后的B通道图。直观来看这四张图分别可以当做是进行了高斯滤波和三个方向sobel算子的结果,如果用简单的灰度图可能会更好。
可以看到,色差很明显,修复也很拉胯,我们来看看DWT究竟是什么样的变换,这里对图片的B通道进行了DWT,其中b是逆DWT之后的B通道图。直观来看这四张图分别可以当做是进行了高斯滤波和三个方向sobel算子的结果,如果用简单的灰度图可能会更好。
 感觉并没有进行频域的变换,就结果图上不像FFT,所以我又试了DCT(离散余弦变换),而且是对YUV而不是RGB空间,使用Y通道(因为人对亮度的微小变化更不明显)
感觉并没有进行频域的变换,就结果图上不像FFT,所以我又试了DCT(离散余弦变换),而且是对YUV而不是RGB空间,使用Y通道(因为人对亮度的微小变化更不明显)
(话说我都没想到要不要试试用YUV进行DWT)
既然加权也可以在变换后比较明显,我决定直接使用加权,解码就是重新进行DCT然后变换、过滤掉一部分值再cmap="rainbow",具体的DCT函数如下:
def DCT(im1,im2,channel=0,rate=0.5):
im2=cv2.cvtColor(im2,cv2.COLOR_RGB2YUV)
imL=list(cv2.split(im2))#分离通道
dct=cv2.dct(np.float32(imL[channel]))#变换
reResult=rate*im1+dct
imL[channel]=cv2.idct(reResult).astype(np.uint8)#逆变换
mixup=np.stack(imL,axis=-1).astype(np.uint8)#重新合成图
mixup=cv2.cvtColor(mixup,cv2.COLOR_YUV2RGB)
#解码(主要就是让内容看的见就行了)
deimL=list(cv2.split(cv2.cvtColor(mixup,cv2.COLOR_RGB2YUV)))#拆分通道
dedct=20*np.log(abs(cv2.dct(np.float32(deimL[channel]))))
return mixup,dedct
显示时我使用了语句进行过滤(具体的参数是试出来的,可以试试别的)
plt.imshow(3*np.maximum(decode-40,0).astype(np.uint8),cmap="rainbow")
下面是处理之后的输出,可以明显的看出,实际上是一堆散点,甚至可以说是噪点,而且Y通道基本上没法解算出来
.png) 所以选了V通道,其中replace是加权之后的,mixup是逆DCT解算出来的V通道
所以选了V通道,其中replace是加权之后的,mixup是逆DCT解算出来的V通道
.png) 然后是将三通道合并的彩色图,其实左上角还是能看出来,有三角形区域的噪声
然后是将三通道合并的彩色图,其实左上角还是能看出来,有三角形区域的噪声
.png) 重新解算出来,然后用上面提到的语句进行显示
重新解算出来,然后用上面提到的语句进行显示
.png) 可以看到效果比较感人,基本上就是啥都看不到
可以看到效果比较感人,基本上就是啥都看不到